Contenu
- Déterminez le temps dans l'air.
- Étape 1
- Étape 2
- Étape 3
- Étape 4
- Déterminez la hauteur maximale
- Étape 1
- Étape 2
- Étape 3
- Déterminez la distance horizontale parcourue.
- Étape 1
- Étape 2
- Étape 3
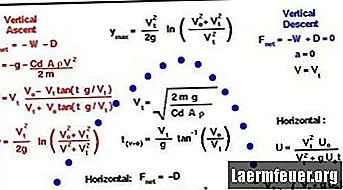
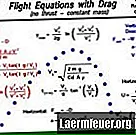
Voici la méthode pour calculer la trajectoire d'une balle et, plus précisément, le temps dans les airs, la portée et le point le plus élevé de sa trajectoire. Dans cet exemple, certaines hypothèses ont été faites pour simplifier le calcul: résistance de l'air négligeable, absence de vent et distance de tir insuffisante pour que la rotation de la Terre prenne effet.
Déterminez le temps dans l'air.
Étape 1
Tout d'abord, la forme de l'arc doit être déterminée. Si l'angle est initialement vers le bas, alors le point le plus élevé est déjà connu pour être la position de tir. Même un angle vers le haut peut avoir la cible comme point le plus élevé, que cet angle soit peu profond ou d'une hauteur suffisante (h). Cela peut être déterminé à l'étape quatre, lorsque le temps d'antenne est déterminé.
Étape 2
Si l'angle "?" la cadence de tir est celle entre la trajectoire initiale du projectile et l'horizontale, donc la vitesse verticale initiale est V (i) = V.sen?.
Étape 3
Le temps dans l'air est calculé en utilisant l'équation de la position h = V.sen? .T - (0,5) g.t ^ 2, où g = 9,8 mètres / secondes ^ 2. Toutes les variables sont connues, sauf le temps dans l'air, t, donc cela peut être résolu en utilisant la fonction quadratique: ax ^ 2 + bx + c = 0, donc, x = [-b ± √ (b ^ 2-4ac )] / 2a
Étape 4
Si plus d'une solution pour t est autorisée, puisque h> 0, alors le premier résultat correspond à quand height = h sur le chemin de montée, et le second à quand height = h sur le chemin de descente. Si h <0, alors la seule solution réelle pour t était autorisée, et l'autre est négative.
Déterminez la hauteur maximale
Étape 1
Si? <0, alors, on sait déjà que la hauteur maximale est la hauteur initiale, h = 0.
Étape 2
S'il y a eu plus d'un temps, t, pendant lequel la balle s'étend h, alors le plus petit t correspond à une trajectoire de vol où h est le point le plus élevé. Le t le plus élevé correspond à la balle atteignant une hauteur plus élevée avant de revenir à h, pour résoudre cette hauteur, utilisez la formule V (t) = V (0) - 9,8t pour trouver la valeur de t lorsque la vitesse verticale est zéro. En d'autres termes, pour quelle heure, t, V.sen? = 9,8t.?
Étape 3
En résolvant t et en reliant la formule de hauteur, nous avons la hauteur maximale: hm = V.sen? - 4,9 t ^ 2. La même approche est utilisée pour la solution de hauteur maximale, si une seule solution pour t était autorisée.
Déterminez la distance horizontale parcourue.
Étape 1
Pour déterminer la distance horizontale parcourue au moment où la balle atteint la hauteur h, calculez d'abord la vitesse horizontale initiale de la balle: v (i) = V.cos (?).
Étape 2
Remplacez le temps, t, lorsque la balle atteint la hauteur finale, A, dans la position de la formule en utilisant la vitesse horizontale: A = V.cosΘ.t. En supposant qu'il n'y a pas de résistance à l'air et pas de terme d'accélération du côté droit.
Étape 3
S'il y a eu plus d'un temps t lorsque la hauteur était en h, alors les deux positions de "A" seront valides, le point le plus élevé atteint étant hm pour le plus petit des deux "A". Les positions finales horizontales et verticales et le point le plus élevé atteint sont maintenant connus, déterminant ainsi la trajectoire de la balle.